Rechenschwäche

Bei Brüchen brech ich ein – Das muss doch nicht sein!
Das Verständnis von Bruchzahlen ist grundlegend für ein erfolgreiches Lernen im Mathematikunterricht am Ende der Grundschulzeit bzw. in den Schuljahren an einer weiterführenden Schule.von Juniorprof. Dr. Silvia Schöneburg, Professur für Didaktik der Mathematik an der Universität Leipzig und Susanne Dögnitz, wissenschaftliche Mitarbeiterin Universität Leipzig, Mathematisches Institut
Das Verständnis von Bruchzahlen ist grundlegend für ein erfolgreiches Lernen im Mathematikunterricht am Ende der Grundschulzeit bzw. in den Schuljahren an einer weiterführenden Schule. Entsprechend stark wird ein Augenmerk darauf gerichtet und intensiv geübt, um die Hürden beim zunächst ungewohnten Vorgehen zu überwinden. Losgelöst von anschaulichen Grundvorstellungen wird die Bruchrechnung jedoch häufig als reines Regelwerk wahrgenommen, das die Kinder nur halb verstehen, auswendig lernen, mit vielen Übungsaufgaben trainieren und nach kurzer Zeit wieder vergessen, weil es nicht verstanden wurde. Die Ausbildung tragfähiger inhaltlicher Vorstellungen ist daher essenziell.
Notwendigkeit der Abstraktion
Kinder bringen aus dem Alltag eigene Erfahrungen zu Bruchzahlen mit. So haben sie Vorstellungen zu konkreten Brüchen wie 1/4 Stunde, 1/2 Meter oder 3/4 Liter. Jedoch heißt dies nicht, dass sie auch wissen, was 1/4, 1/2 usw. losgelöst von diesen Größen bedeuten. Das Wissen um eine Viertelstunde bedeutet noch nicht das Verständnis von 1/4 als Teil eines Ganzen. Erst die Abstraktion von speziellen Größeneinheiten auf eine allgemeine Bezugsgröße, das Ganze, ermöglicht ein inhaltliches Verständnis für Bruchzahlen. Dieses Verständnis bildet die Grundlage für die spätere systematische Auseinandersetzung mit Brüchen und deren Rechengesetzen bezüglich der Grundrechenarten. Dass Alltagsvorstellungen durchaus auch zu Verwirrung führen können – insbesondere dann, wenn sie mit mathematischen Konzepten kollidieren –, zeigt folgendes Beispiel von Nadja (6. Klasse): Welcher Teil ist gefärbt?
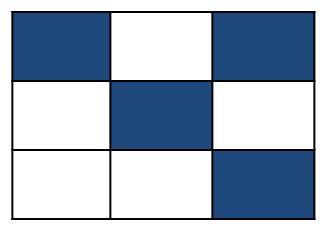
Antwort: 4/5 Nadja erkennt die Anzahl der blauen und weißen Kästchen vollkommen richtig. Sie deutet die Darstellung als Verhältnis, so wie sie es aus dem Alltag, z. B. bei der Darstellung von Torverhältnissen, gewohnt ist und erhält das Ergebnis 4 zu 5, das sie fälschlicherweise als 4/5 interpretiert. Sie erkennt nicht das Ganze, die 9 Kästchen, von denen 4 markiert sind. Ihr sind die Gemeinsamkeiten und Unterschiede zwischen den verschiedenen Betrachtungsweisen 4 zu 5, 4 von 5 sowie 4 von 9 noch nicht bewusst.
Inhaltliche Grundvorstellungen zu Bruchzahlen, insbesondere der Bruch als Teil eines Ganzen, sind jedoch zur weiteren Auseinandersetzung mit den Bruchzahlen unabdingbar. Denn nur mithilfe dieser ist es möglich, das Konzept der Gleichwertigkeit von Brüchen, aber auch die Grundrechenoperationen im Bereich der gebrochenen Zahlen zu verstehen.
Unterschiede zwischen Brüchen und natürlichen Zahlen verstehen
Brüche können im Gegensatz zu den natürlichen Zahlen nicht nur auf eine Weise beschrieben werden. Denn es macht für die numerische Größe des Bruchs keinen Unterschied, ob ich 4 von 9 Teilen oder 8 von 18 Teilen markiert habe. Damit einhergehend wird auch klar, dass Brüche im Gegensatz zu den natürlichen Zahlen keinen direkten Vorgänger oder Nachfolger besitzen, sondern zwischen zwei Brüchen immer noch ein weiterer gefunden werden kann. Kinder, die bisher hauptsächlich mit zählenden Rechenstrategien gearbeitet haben, bekommen nun große Probleme, sich den Zahlbereich der gebrochenen Zahlen mit dieser Methode zu erschließen.
Aber auch nicht zählende Rechner scheitern häufig bzw. haben große Probleme bei der Auseinandersetzung mit Brüchen, insbesondere bei den Grundrechenoperationen, da der neue Zahlbereich eine veränderte Herangehensweise erfordert. Beispielsweise muss die Vorstellung, dass die Multiplikation immer vergrößert (außer bei 0 und 1), aufgegeben werden. Dabei muss eine Umdeutung der Multiplikation im Bereich der gebrochenen Zahlen stattfinden. Die Multiplikation als wiederholte Addition ist nur noch für den Spezialfall der Multiplikation einer natürlichen Zahl mit einer gebrochenen Zahl gültig.
„Von-Ansatz“
Wie sieht es aber bei zwei gemeinen Brüchen aus? Der „Von-Ansatz“ ermöglicht hier das Entwickeln tragfähiger inhaltlicher Vorstellungen. So wird die Multiplikationsaufgabe 2/3 * 5/6 als 2/3 von 5/6 gedeutet. Der erste Faktor wird als Anteil vom zweiten Faktor betrachtet. Es geht also um das Bilden von Bruchteilen von Bruchteilen. Dies kann für die Schülerinnen und Schüler gut handelnd (mithilfe von Papierfalten) bzw. bildlich veranschaulicht werden:
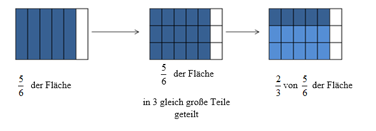
Durch das Rechteckschema lässt sich verdeutlichen, was 2/3 von 5/6 bedeutet. Dafür werden 5/6 noch einmal in drei gleich große Teile geteilt. Davon werden nun zwei Drittel genommen und das Ergebnis kann durch das Identifizieren des nun entstandenen Bruchs ermittelt werden. Mithilfe dieses Modells erklärt sich auch, dass die Multiplikation nicht immer vergrößern, sondern durchaus auch verkleinern kann. So werden Fehler wie der folgende von Nadja vermieden:
3/4 * 2/5 = 15/20 * 8/20 = 6
Nadja hat die Multiplikationsaufgabe ohne das Verständnis des „Von-Ansatzes“ bearbeitet. Ihr schienen vor allem noch die Regeln zur Addition zweier gemeiner Brüche im Gedächtnis zu sein, die sie hier auch auf die Multiplikation angewendet hat. Dabei hat sie die beiden Zähler nach dem Erweitern multipliziert und den gemeinsamen Nenner beibehalten, ohne das Ergebnis anschließend zu hinterfragen. Denn, dass Multiplikation vergrößert, ist ihr intuitiv aus den natürlichen Zahlen bekannt.
Eine häufige und wiederholte Einbeziehung einer Grundvorstellung zu Brüchen mindert die Gefahr, dass Regeln unreflektiert verallgemeinert werden, und hilft den Kindern dabei, ohne „Einbrüche“ weiterzulernen.
Autorinnen

 Susanne Dögnitz (links) und Dr. Silvia Schöneburg (rechts)
Susanne Dögnitz (links) und Dr. Silvia Schöneburg (rechts)
Meist gelesen




