Rechenschwäche
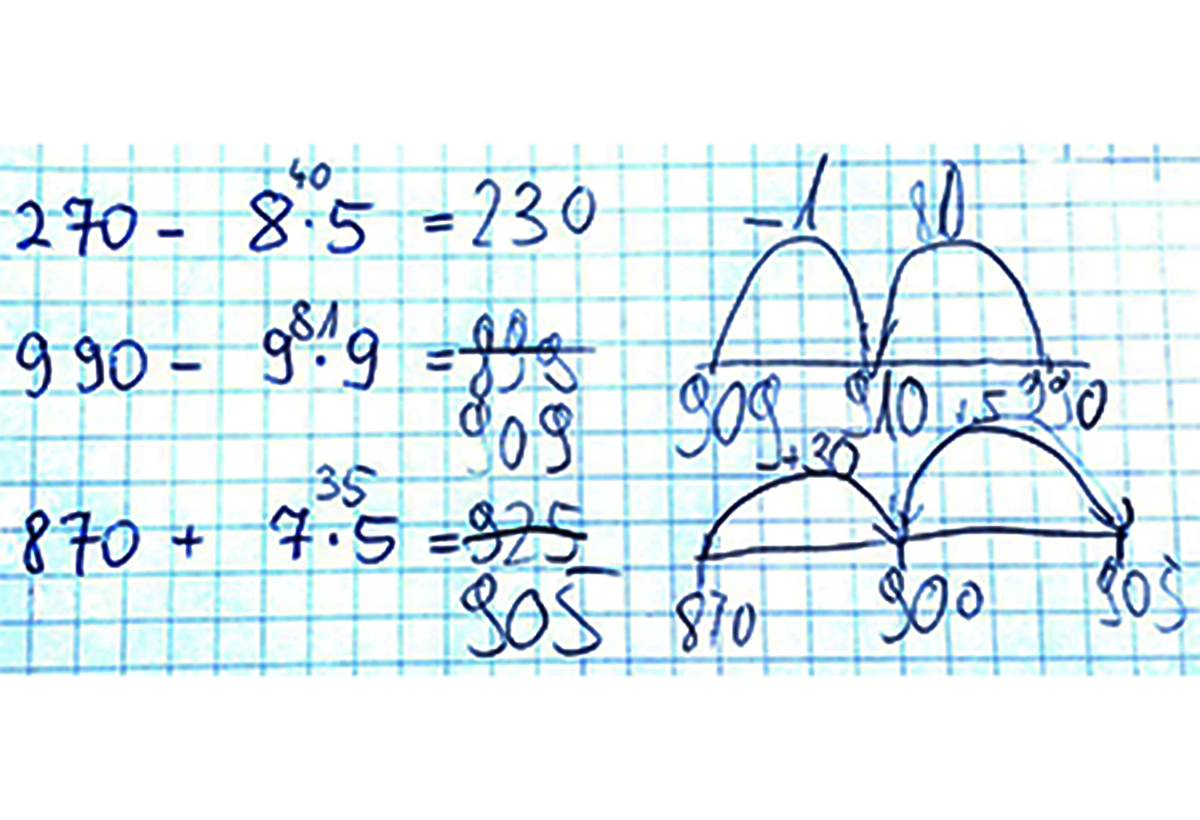
Nachteilsausgleich bei besonderen Schwierigkeiten im Rechnen
In seinem Beitrag geht Dr. Christian Werge auf die Möglichkeiten und Herausforderungen eines Nachteilsausgleichs im Matheunterricht ein.Von Dr. Christian Werge, stellv. Institutsleiter im Fachbereich Rechenschwäche des Duden Instituts für Lerntherapie Halle (Saale)
Sowohl in der täglichen Arbeit als Lerntherapeut als auch bei Diskussionen mit Lehrerinnen und Lehrern begegnet uns häufiger die Frage, wie Kinder mit Lernschwierigkeiten im Unterricht wirksam unterstützt werden können. Dies steht in engem Zusammenhang mit der Frage nach einem Nachteilsausgleich wegen der besonderen Schwierigkeiten im Fach Mathematik (auch als „Rechenschwierigkeiten“ oder „besondere Schwierigkeiten im Rechnen, bSR“ bezeichnet). Im Folgenden werden Möglichkeiten und Herausforderungen verschiedener Formen eines Nachteilsausgleichs erörtert.
1. Bereitstellen zusätzlicher Anschauungs-, Informations- und Lernmittel
Schülerinnen und Schülern wird z. B. gestattet, bei Schwierigkeiten bei Plus- und Minusaufgaben im Zahlenraum bis 20 ein gewöhnliches Lineal zu benutzen. Auch das Hunderterfeld, das zweifellos die Struktur des Dezimalsystems gut abbildet, kann abzählend zum Rechnen eingesetzt werden. Tatsächlich gelingen dadurch fehlerfreie Teilrechnungen, auch beim schriftlichen Addieren und Subtrahieren. Aber helfen wir dem betroffenen Kind wirklich? Fördern und festigen wir damit nicht ungeeignete Rechenstrategien, insbesondere das zählende Rechnen? Schon vor 25 Jahren, im „Handbuch des Förderns im Mathematikunterricht“, sprechen Lorenz/Raddatz von einer „Sackgasse …, aus der die Kinder im 2. und 3. Schuljahr nicht mehr herauskommen“. Aber auch Sekundarschüler/-innen „greifen immer noch häufig zu zählenden Lösungsstrategien (und) zeigen gravierende Defizite im Verständnis des Dezimalsystems“, wie Gaidoschik schrieb.
Als einen möglichen Ausweg sehen wir den „Rechenstrich“ (Abb. 1) an, einen unbeschrifteten Zahlenstrahl, an dem die Operanden von Additions-, Subtraktions- und auch Ergänzungsaufgaben notiert werden. Er erfüllt auch die Forderung nach Notizen (auf einem „Schmierzettel“) bei etwas komplexeren Kopfrechenaufgaben und verschafft eine höhere Sicherheit sogar im Hinblick auf „Zahlendreher“ (bei Orientierungsschwierigkeiten).
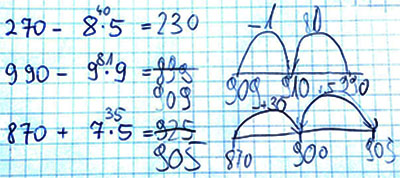 Abb. 1
Abb. 1
Ebenso hat eine Einmaleinstafel (vgl. Stoye) für betroffene Kinder viele Vorteile: Erfahrungsgemäß kann sie problemlos im Klassenzimmer aufgehängt und von allen Schülerinnen und Schülern verwendet werden. Die leistungsstärkeren unter ihnen werden sie nicht weiter beachten, manche werden sie nur für die „schweren“ Aufgaben wie „7 · 8 = 56“ benutzen, die sie noch nicht ganz automatisiert haben. Die betroffenen Schüler lesen Ergebnisse ab, mit der Hoffnung, dass sich Behaltenseffekte einstellen.
Zu nennen sind auch spezielle Formelsammlungen, orientiert an Lehrmaterialien für die Berufsschule. Diese Bücher stellen viele Formeln, jeweils aufgelöst nach einer der beteiligten Größen, bereit. Das Vorgehen wird folgendermaßen eingeordnet: „Die Formelsammlung unterscheidet sich von den gebräuchlichen Formelsammlungen dadurch, dass der Lernende selbst überprüfen kann, ob er seine Formel richtig umgestellt hat – er vergleicht! Somit wird dem Lernenden die Unsicherheit genommen und der Wille gefördert, zügig zum richtigen Ergebnis zu gelangen.“
Auch Apps können ein Hilfsmittel sein. Beispielsweise berechnet „photo math“ nicht nur verzwickte Terme aus Zahlen, sie gibt auf Tastendruck auch alle Teilschritte, jeweils farbig markiert, wieder.
2. Nutzung von Merkhilfen ermöglichen
Ebenso kann es Kindern mit Lernschwierigkeiten helfen, wenn sie Merkhilfen für bestimmte Rechenoperationen kennen und diese im Unterricht auch anwenden dürfen.
Beispiel: Die KlaPPS-Regel – eine Merkhilfe für die Vorrangregeln aus den Erfahrungen der Lerntherapie
Schon für Rechenaufgaben (Terme) mit drei Operanden muss geklärt werden, in welcher Reihenfolge gerechnet werden soll. Viele Schüler/-innen mit Lernschwierigkeiten verfahren zunächst einmal nach der Regel „von links nach rechts“. Die Vereinbarung „Punktrechnung vor Strichrechnung“ ist den meisten Lernenden in der Formulierung bekannt, aber nicht in ihrer Bedeutung. Oft muss angeschaut werden, welche Operanden durch eine Punktrechnung miteinander verknüpft sind und welche durch eine Strichrechnung. Klammern setzen die Regel „Punkt vor Strich“ außer Kraft.
Die notierte KlaPPS-Regel (Abb. 2) hilft daran zu denken, dass zuerst Klammern, dann Potenzen, dann Punktrechnungen und schließlich Strichrechnungen zu erledigen sind.
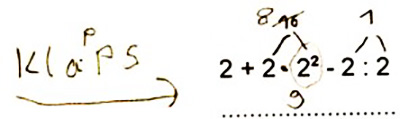 Abb. 2
Abb. 2
3. Mehr Bearbeitungszeit
Das Einräumen einer verlängerten Bearbeitungszeit in Leistungskontrollen wird häufig angewendet. Schwierigkeiten dabei macht der Rhythmus der Unterrichtsstunden, sodass Schüler/-innen ggf. bis in die Pause oder bereits in einem Teil der folgenden Unterrichtsstunde an ihrem Test sitzen. Darüber hinaus haben auch Aufmerksamkeits- und Konzentrationsspanne diesen Rhythmus, sodass die Verlängerung oft nicht hilfreich ist.
Dagegen bietet das (unproblematische) Streichen von Aufgaben oder Teilaufgaben, ggf. unter Beachtung unterschiedlicher Anforderungsbereiche, auch einen psychologischen Effekt. Die Erfolgserwartung steigt und die Misserfolgsorientierung wird zurückgedrängt. In einer Kontrollarbeit einer 2. Klasse (Abb. 3) hat die Lehrerin zusätzlich auf Richtungsprobleme vorbereitet.
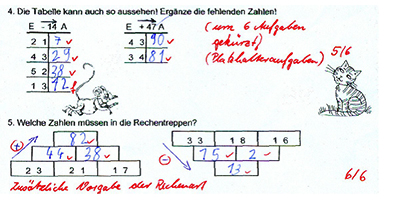 Abb. 3
Abb. 3
4. Alternative Formen der Leistungserhebung
Meist wird hier an „mündlich statt schriftlich“ gedacht, was mit Blick auf den betroffenen Schüler/die betroffene Schülerin und seine/ihre Möglichkeiten, sich sprachlich zu äußern, differenziert gesehen werden muss. In der „Verwaltungsvorschrift …“ aus Mecklenburg-Vorpommern wird vorgeschlagen, „Leistungserhebung über Aufgabentypen mit geringem Schreibaufwand [zu] realisieren, z. B. Multiple Choice, Zuordnungen, Reihenfolgen, Nummerierungen, Lückentexte, Markieren/Strukturieren, grafische Umsetzung“. Das ist natürlich mit einem höheren Aufwand für den Lehrer/die Lehrerin verbunden. Andere erprobte Vorschläge sind „längerfristige Vereinbarungen zu kompakten mündlichen Leistungsdarstellungen“, z. B. in Vorträgen zu Teilaspekten des Stoffgebiets oder auch zu angrenzenden Themen. Dagegen kann ohne zusätzlichen Aufwand eine „Benotung von Leistungen in geöffneten Unterrichtsformen (z. B. eigenständige Planung, Problemlösestrategien und Methodenwissen)“ (ebenda S. 16) erfolgen.
Fazit: Nachteilsausgleich ersetzt kein pädagogisches Handeln
Neben den bereits genannten Formen des Nachteilsausgleichs sollten auch die psychologischen Faktoren im Lernprozess nicht außer Acht gelassen werden: Es ist ebenso wichtig, dem/der Lernenden auch kleine Lernfortschritte deutlich zu machen sowie ermutigende Formen der Fehlerrückmeldung zu finden. Dabei spielen auch Lob und Ermunterung durch die Körpersprache des Lehrers/der Lehrerin eine große Rolle. Der Lernerfolg kann umso größer ausfallen, wenn individuelle Lern- und Hausaufgaben für Kinder mit Lernschwierigkeiten gefunden werden (vgl. Kultusministerium Sachsen, S. 29).
Eine enge und vertrauensvolle Zusammenarbeit aller am pädagogischen Prozess beteiligten Lehrer/-innen, Psychologen/Psychologinnen und Mitarbeiter/-innen der Schulverwaltungen ist daher unbedingt zu empfehlen, um die betroffenen Schülerinnen und Schüler zu erfolgreichem Lernen zu befähigen.

Dr. Christian Werge war langjähriger Mitarbeiter im Bereich Mathematikdidaktik an der Universität Leipzig und arbeitet heute unter anderem als Lerntherapeut am Duden Institut für Lerntherapie Halle (Saale).
Literatur
Förderung von Schülerinnen und Schülern mit besonderen Schwierigkeiten im Lesen, im Rechtschreiben oder im Rechnen. Verwaltungsvorschrift des Ministeriums für Bildung, Wissenschaft und Kultur. Mitteilungsblatt des Ministeriums für Bildung, Wissenschaft und Kultur Mecklenburg-Vorpommern Nr. 5/2014
Formeln und Tabellen für metalltechnische Berufe – mit umgestellten Formeln, Qualitätsmanagement und CNC-Technik. (Autor: Schierbock, P.; 18. Auflage) Kindle Edition. Bildungsverlag Eins, Köln 2015
Gaidoschick, M. (2008): Rechenschwäche in der Sekundarstufe: Was tun? Journal für Mathematik-Didaktik, 29 (3/4), 287–294
Handreichung zur sonderpädagogischen Förderung in Sachsen-Anhalt. Richtlinien – Grundsätze – Anregungen. Kulturministerium Sachsen-Anhalt, Magdeburg, o. J. (etwa 2010)
Lorenz, J. H.; Radatz, H.: Handbuch des Förderns im Mathematikunterricht. Hannover: Schroedel 1993
Stoye, W.: Malfolge-Plakat. http://www.wernerstoye9.de/Malfolge-Plakat [12.03.2019]
Werge, Ch.: Hilfen für Schüler der Sekundarstufe mit besonderen Schwierigkeiten im Rechnen: Erfahrungen mit der KlaPPS-Regel in der Lerntherapie. In: Beiträge zum Mathematikunterricht 2016. Vorträge auf der 50. Tagung für Didaktik der Mathematik 2016 in Heidelberg. WTM Verlag, Münster 2016, S. 1047–1050
Meist gelesen




